ФОРМИРОВАНИЕ РЕЗУЛЬТАТОВ ПОВТОРНЫХ ИСПЫТАНИЙ

Сравнение результатов двух повторных испыта

При проведении повторных испытаний однотипной продукции имеет место проблема воспроизводимости, в связи с чем появляется необ­ходимость расчета, нормирования и оценки расхождения результатов таких испытаний [31]. При этом под воспроизводимостью результа­тов понимают такое их свойство, когда каждый повторный результат статистически незначимо отличается от предыдущего (термин «зна­чимость» — по ГОСТ 15895-77). Одной из задач этой проблемы яв­ляется выбор и стандартизация показателей воспроизводимости ре­зультатов повторных испытаний.

В [42] обосновано предположение об индивидуальности распре­делений результатов повторных испытаний. Действительно, так как в зависимости от вида повторных испытаний, т. е. от того, где и в каких условиях они проводятся (в одной и той же лаборатории, в одинаковых условиях, одними и теми же методами, средствами и испытателями или в различных лабораториях, в различных условиях, различными средствами и методами), результаты этих повторных ис­пытаний могут иметь различное распределение или при одинаковых видах распределения — существенно различные параметры. А это означает статистическую неоднородность получаемых при испытани­ях результатов [84]. Поэтому оценка воспроизводимости должна сво­диться к известной в статистике задаче проверки гипотезы о тожде­ственности законов распределений — гипотезы однородности результатов, а показатели воспроизводимости целесообразно искать среди мер близости законов распределений этих результатов (так на­зываемых критериев однородности) [41].

Рассмотрим этот вопрос на основе анализа применяемых на прак­тике параметрических и непараметрических критериев однородности.

Параметрические критерии требуют большего количества апри­орной информации, в частности необходимо знать вид сравниваемых законов распределения. Задача проверки гипотезы однородности сво­дится к задаче проверки равенства параметров этих распределений.

Для нормального распределения все применяемые критерии можно свести к четырем случаям (табл. 12.1). Первые три из них относятся

ON NJ oo

Критерии проверки однородностей двух нормальных распределений № Гипотеза Априорная информация Статистика Решающее правило Возможные показатели воспроизводимости I Сравнение математи­ ческих ожиданий И <*2 известны (*1 — х1)-(М1 — М2) М1П1+<^.1П2 ft — ^1 ^ гг2 №l"i+<%l"l 1-4/2 1*т — ч „ *і *1 = ^1-а/2 V°1 / «1 + °2 / "2 II _2 _п1 °1 "°2 неизвестны {Ъ-Зд-Шу-Мд Syjl/Пу +1/«2 s (ц-1)5?+(я,-1)5? /І1 + /І2 — 2 ft " *2І ^2 57l//^+l/^ ‘"“Z2 *1 ^1 = *l-a/2^V^ / Л1 + 1 / ^2 III Oj Ф о2 неизвестны (х, — Xj) — (Af, — Л/2) т.2 ‘la/lWtf, + ! t-aJ2^nl>Sl «2 ft — ^2 Is Tl-aJ2 ft — *2І. _ *1 ’ ^1 = ^l-a/2 IV Сравнение дисперсий S{ и S2 известны sh Sl/o Si /s2 ^ 5і2 / S2 . *2 ’ *2 = ^1-a

 

к проверке гипотезы о равенстве математических ожиданий. В пер­вом случае предполагается, что дисперсии Oj и исходных сово­купностей сравниваемых выборок объемом п1 и л2 известны, во вто­ром — дисперсии равны, но не известны, в третьем — дисперсии не равны и не известны. Четвертый случай предусматривает сравнение дисперсий.

Для каждого случая в табл. 12.1 приведены рабочие формулы для определения статистики критерия и решающих правил, где: хх и х2 — выборочные средние повторных испытаний; S? и Si — выборочные дисперсии; М{ и М2 — сравниваемые математические ожидания; Uy, t и R — квантили стандартных распределений нормального, Стьюден — та и F — распределения Фишера при доверительной вероятности у [41, 74].

Поскольку все приведенные выше статистики I—III основаны на сравнении выборочных средних, имеющих в силу центральной пре­дельной теоремы асимптотически нормальное распределение для лю­бого распределения исходных генеральных совокупностей, то эти ста­тистики оказываются мало чувствительными к отклонениям от нормальности. Поэтому они могут применяться для оценки воспро­изводимости на уровне средних для широкого класса одномодальных распределений.

В отличие от указанных выше статистик статистика для сравне­ния дисперсий (IV) чувствительна к отклонениям от нормальности. Однако и она имеет асимптотически нормальное распределение, хотя и отличное от того, которое имеет место при нормальном распреде­лении.

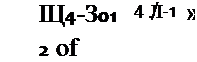В том случае, когда распределение исходной совокупности изве­стно, представляется возможным использование приведенной статис­тики при измененном числе степеней свободы п{ и равных [38]

где щ — четвертый момент распределения. Для гІ2 формула анало­гична.

Анализируя рассмотренные выше статистики, нетрудно заметить, что в качестве показателей воспроизводимости целесообразно исполь­зовать:

• нормированный модуль разности выборочных средних:

Ах = хх — х2К{ (12.1)

• нормированное отношение выборочных дисперсий

= S? {S]K2)"‘, (12.2)

и (или) уровень значимости а, где Кх и К2 — коэффициенты (см. табл. 12.1).

Первые два показателя (Дх и s*) имеют ясный физический смысл и не требуют пояснений. Возможность применения третьего показа­теля для оценки воспроизводимости объясняется следующим.

Уменьшая уровень а в решающих правилах (см. табл. 12.1), все­гда можно добиться принятия гипотезы однородности, причем боль­шим расхождениям между х{ и х2 или S* и S2 (плохая воспроизво­димость) будут соответствовать малые уровни значимости. При этом минимальная величина уровня значимости, при котором для опреде­ленных значений Х, х2, Si, S2 будет выполняться условие однород­ности, может быть принята в качестве критического значения пока­зателя воспроизводимости. Соответствующие этому значению расхождения результатов испытаний называют критическими. В этом случае с вероятностью а результаты испытаний относятся к одному закону распределения.

Непараметрические критерии (расстояния, перестановок, ранго­вые) не требуют знания законов распределения исходных совокупно­стей, однако они более трудоемки в вычислениях и индивидуальны по отношению к различным видам неоднородности. Кроме того, они требуют таблиц специальных распределений, которые имеются лишь в узкоспециальных изданиях и для практических целей недостаточно полны. Поэтому из всего многообразия непараметрических критери­ев рассмотрим лишь те, статистики которых вычисляются достаточно просто и (или) допускают нормальную аппроксимацию. Основные характеристики этих критериев сведены в табл. 12.2, где m-Jn — ча­стота попадания исследуемой величины в интервальный вариаци­онный ряд; Pi — теоретическое значение вероятности попадания слу­чайной величины в этот интервал; г — число интервалов (г > 8); и — объем выборки.

Критерии расстояния (Смирнова, % ) используют в качестве ра­бочих статистик различные меры расстояния между сравниваемыми функциями распределения и при достаточном объеме выборки (п > 50) позволяют обнаружить практически любое отличие между ними [77]. Критерий Смирнова основан на сравнении функций рас-

пределения Flni (Х[ ), F2„2 (х2 ) двух выборок {*„}, {х2,} объемом л, и п2 соответственно. При этом большой объем вычислений при исполь-

Непараметрические критерии однородности Группа критериев Вид критерия Статистика критерия Решающее правило Критерии расстояния Колмогорова- Смирнова = SUP K(*l>-V*2>| xl’~x2 D>Vh-D-a ^2[ Ы 2 ‘ І + 1 | Л+Л2Ц X2 Критерии перестановок Знаков Число знаков т /2 1 ГП— + — 2 2 ^l-a/2 Серий Число серий г г 2я1«2 . 1 2 2 Г2л,«2 /гг1 ^ п Уп О./! Инверсий Число инверсий А ^-л(и-1) + 1 2 2 і /й(й-1) [2 2 -1 5 ^1-0/2 Инверсий упрощенный Число инверсий А* Л* П і -2*4 < их_ф Ранговые критерии Сиджела—Тьюки Сумма рангов меньшей выборки |Л| -0,5^(л, +«2 +1) + 0,5| ^ ^[л, Л2(л, + «2 +1)] 1 /12 1-01/2 Манна—Уитни Сумма рангов для одной из выборок -0,5^(л,+/»2+ 1)+0,5| ^ л/[лІл2 ("ї + «2 + О] 1 /12 1-0/2 Уилкинсона («і=«2) То же -О. бл^л, + /*2 +1) + 0,5| ^ ^[й, й2(и, + й2 + л2)] 1/12 1-0/2

зовании данного критерия связан с необходимостью построения ва­риационных рядов и пропорционален квадрату объема выборки. При п2 -> °° критерий Смирнова трансформируется в критерий Колмого­рова, требующий знания так называемого эталонного распределения [77]. Критерий также требует знания эталонного распределения, однако он не нуждается в построении упорядоченных вариационных рядов, поэтому более экономичен в вычислительном отношении. Кроме того, квантиль X2 — распределения допускает нормальную апп­роксимацию [77] и позволяет проверить гипотезу однородности, ког­да эталонное распределение известно с точностью до к параметров, оцениваемых по той же выборке. В этом случае число степеней сво­боды выбирается равным г-к-1, а неизвестные параметры оценива­ются методом «минимум X ».

Критерии перестановок (знаков, серий, инверсий) используют тот факт, что при выполнении гипотезы однородности все переста­новки упорядоченных значений смеси случайных величин из двух выборок равновероятны. При применении этих критериев последо­вательности сравниваемых результатов испытаний {*ц}, {*2, } объе­диняют в одну последовательность {*,-}.

Статистикой критерия знаков является число случаев, когда

гДе *о — некоторая заданная величина (например, медиана). Эта статистика при фиксированном объеме объединенной выборки п имеет биномиальное распределение, а задача проверки гипотезы од­нородности сводится к задаче проверки гипотезы о значении пара­метра биномиального распределения = 0,5. Статистикой критерия серий является общее число серий г в объединенной упорядоченной в порядке возрастания последовательности, т. е. число последователь­ных данных из первой и второй выборок [94].

Статистикой критерия инверсий является общее число инверсий А в объединенной неупорядоченной последовательности, т. е. число случаев, когда последующий член статистического ряда меньше пре­дыдущих членов этого ряда. Задача проверки гипотезы однородности в этом случае так же, как и для критериев знаков, сводится к задаче проверки гипотезы о параметре биномиального распределения р = 0,5 [37]. При необходимости сокращения вычислительных затрат исполь­зуется также упрощенный критерий инверсий, когда последователь­ный член ряда сравнивается не со всеми предыдущими членами, а только с соседним [37].

Ранговые критерии (Сиджела-Тьюки, Манна-Уитни, Уилкинсо­на) применяются в тех случаях, когда удобно использовать не сами результаты испытаний, а их ранги при расположении данных в опре­
деленном порядке. При применении этих критериев последователь­ности сравниваемых данных {*j}, {х2} объединяют в одну упорядо­ченную в порядке возрастания последовательность. Статистикой кри­терия Сиджела-Тьюки является сумма рангов для выборки меньшего объема причем ранг 1 приписывается наименьшему значению, ранг 2 — наибольшему, ранг 3 — предыдущему наибольшему и т. д. Статистикой критерия Манна-Уитни является сумма рангов для од­ной из сравниваемых выборок при расположении объединенной пос­ледовательности в порядке возрастания [93]. Критерий Уилкинсона является частным случаем критерия Манна-Уитни при пх = и2 [93].

Критерии знаков, инверсий и Манна-Уитни позволяют обнару­жить монотонные изменения в функциях распределения. Критерий серий позволяет обнаружить колебательный тренд, критерий Сидже — ла-Тьюки используется для проверки воспроизводимости по диспер­сиям. Ранговые критерии и критерии перестановок можно приме­нять даже при малых выборках (п < 10), при п £ 10 все они допускают нормальную аппроксимацию.

Перечисленные непараметрические критерии требуют наличия таблиц специальных распределений достаточной для практики пол­ноты, а также сравнительных характеристик по мощности и эффек­тивности критериев, позволяющих произвести рациональный выбор того или иного критерия.

В отечественной и зарубежной литературе вопросы мощности и эффективности непараметрических критериев освещены недостаточ­но полно и сводятся в основном к сравнению эффективности этих критериев с соответствующими параметрическими критериями, ис­пользуемыми для нормального распределения. Ниже приведены зна­чения асимптотической относительной эффективности (АОЭ) ряда непараметрических критериев для нормального распределения:

Критерий АОЭ

Знаков………………………………………………………………………. 0,63

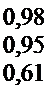Инверсий………….

Манна—Уитни … Сиджела—Тьюки

Однако АОЭ, например, критерия Манна-Уитни для у-распре — деления равна 3, для логистического распределения — 1,1, для пря­моугольного распределения — 1 и для любого распределения не ме­нее 0,864.

Предлагаемый подход заключается в замене непараметрического критерия эквивалентным параметрическим, не требующим предва­рительного предположения о нормальности, и последующей нормаль­
ной аппроксимации этого критерия с целью аналитического опреде­ления его мощности и эффективности.

Для рассмотренных выше критериев эквивалентный параметри­ческий критерий может быть построен с использованием биномиаль­ного распределения с одним и тем же значением его параметра. Про­иллюстрируем предлагаемый подход на примере наиболее простого критерия знаков.

Статистикой критерия знаков является число случаев т, когда выборочное значение оказывается больше некоторой фиксированной величины. В качестве этой величины чаще всего используют выбо­рочную медиану. Тогда для объема выборки п статистика критерия имеет биномиальное распределение, а задача проверки гипотезы од­нородности сводится к задаче проверки гипотезы о заданном значе­нии параметра биномиального распределения р = 0,5.

Используя нормальную аппроксимацию с поправкой на непре­рывность, получим решающее правило для принятия гипотезы одно­родности в виде неравенства

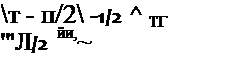а/2’

где U^_aj2 — квантиль стандартного нормального распределения уровня

значимости а/2. Мощность критерия в этом случае может быть запи­сана в аналитическом виде:

т[^-0,5)-Уа/2/2| №,-0,5)+ ^,/2]

1 JP(P ~ 1) J 1 УІРІР" 1) J

Как видно из приведенного выражения, мощность критерия яв­ляется функцией трех аргументов: размера критерия а, «расстоя­ния» между проверяемой и альтернативной гипотезами и объема вы­борки п. Если бы удалось зафиксировать «расстояние» между проверяемой и альтернативной гипотезами для ряда критериев, то для сравнения мощности и относительной эффективности этих кри­териев заданного размера достаточно было бы сопоставить необходи­мые объемы выборок.

Анализ перечисленных выше критериев позволяет произвести такую фиксацию «расстояния» между проверяемой и альтернативной гипотезами. Так, например, статистикой критерия инверсий явля­ется сумма числа инверсий А членов неупорядоченного статистичес­кого ряда, составленного из ординат случайного процесса:

Л = Х X U(xi, Xj),

/=1 j=i+1

Эта величина также имеет биномиальное распределение, не за­висящее от характера исходного распределения, со средним значе­нием и дисперсией:

M[A = Np; D[A] = Np(l-p),

где р — вероятность появления инверсий при единичном наблюде­нии; N = п(п-1)/2. Нулевой гипотезе однородности, как и для кри­терия знаков, соответствует значение параметра биномиального рас­пределения р = 0,5.

Следовательно, для сравнения мощности и относительной эф­фективности этих критериев достаточно сравнить эффективные числа измерений.

В задачах оперативной обработки измерительной информации часто используют упрощенный критерий инверсий, когда каждое вновь поступившее измерение сравнивается не со всеми предыдущими, а только с соседними. Эффективное число измерений для этого кри­терия N = п -1. Аналогичные рассуждения можно провести относи­тельно критериев Манна-Уитни и его частного случая — критерия Уилкинсона, а также критерия Сиджела-Тьюки. Статистиками этих критериев являются суммы рангов выборок меньшего объема при объе­динении двух сравниваемых выборок в порядке возрастания их эле­ментов. Эти статистики имеют одно и тоже распределение, хотя ранжирование при использовании критериев Манна-Уитни (Уилкин­сона) и критериев Сиджела-Т ьюки различно.

Ниже приведены формулы для расчета эффективного числа из­мерений N в случае использования различных критериев при одном и том же объеме выборки.

1 при Xj > Xj О при X; 2 X, 4 I *

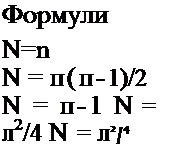
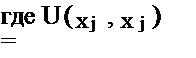Критерий

Знаков ………………………..

Инверсий…………………….

Инверсий упрощенный

Уилкинсона ………………..

Сиджела—Тьюки………..

Итак, на основе предложенного подхода можно рекомендовать критерий инверсий, обеспечивающий заданную мощность при наи­меньшем объеме выборки.

Анализ непараметрических критериев однородности показывает, что сами статистики этих критериев не позволяют сформулировать
удобные показатели воспроизводимости, так как не имеют физичес­кого смысла. Наиболее рациональным и общим показателем воспро­изводимости в данном случае может служить уровень значимости.

Таким образом, применение методов математической статисти­ки при проведении испытаний продукции позволяет одновременно с проверкой однородности результатов повторных испытаний на осно­ве использования известных статистических критериев проводить оцен­ку воспроизводимости этих результатов. В качестве показателей вос­производимости удобно использовать: нормированный модуль разности выборочных средних (12.1), называемый интервалом воспроизводимо­сти’, нормированное отношение выборочных дисперсий (12.2), назы­ваемое коэффициентом разброса воспроизводимости и (или) уровнем значимости (12.3). При этом в случае отсутствия априорной инфор­мации о виде и параметрах законов распределения результатов испы­таний для оценки воспроизводимости желательно использовать уро­вень значимости. Результаты повторных испытаний целесообразно считать воспроизводимыми, если они статистически однородны при выбранном значении уровня значимости.

При появлении информации о виде и (или) параметрах законов распределения результатов, если уровень значимости 0,05<а<0,5, целесообразно дополнительно использовать интервал воспроизводи­мости или (и) коэффициент разброса воспроизводимости. Такая двух­этапная процедура оценки воспроизводимости потребует небольших дополнительных расчетов.